Recursive Call রিকার্সিভ কল
 রিকার্সিভ কল
রিকার্সিভ কল
আমরা অনেক প্রোগ্রামের প্রয়োজনে বিভিন্ন সময় রিকার্শন ব্যবহার করে থাকি যেমন – কোন নাম্বারের ফ্যাক্টোরিয়াল বের করা, ফিবোনাচ্চি/ফিবোনাক্কি নাম্বার বের করা, GCD নাম্বার বের করা, ইত্যাদি। কিন্তু রিকার্শনের মাধ্যমে একটা নাম্বারের জন্য কোন রেজাল্ট পাওয়ার জন্য আমাদের লেখা ফাংশনটা মোট কয়বার কল হচ্ছে সেটা বের করি না, কিংবা বের করার দরকার হয় না। এই পোষ্টটা লেখার প্রধান উদ্দেশ্য হল ফিবোনাচ্চি নাম্বার বের করার সময় একটা ফাংশন মোট কতবার কল হয় সেটা দেখা এবং C/C++ এবং Java তে কিভাবে ইম্পিমেন্ট করতে হত সেটা শিখা।
ফিবোনাচ্চি নাম্বার বের করার সূত্র হলঃ
ফিবোনাচ্চি নাম্বার বের করার সূত্র হলঃ
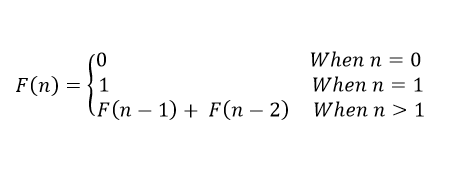
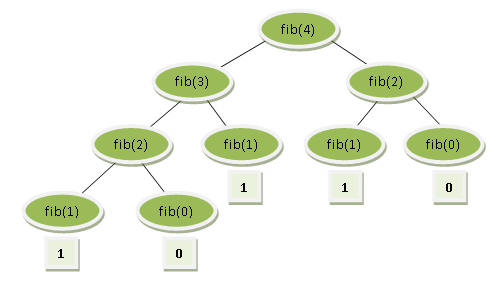
ছবিটি URI Online Judge থেকে নেওয়া হয়েছে
যখন নাম্বারটা 1 থেকে বড় তখন আমাদেরকে গুনতে হবে মোট কয়বার ফাংশনটা কল হচ্ছে। উপরের ছবিতে আমরা দেখতে পারছি মোট ৮ বার কল হয়েছে। কিভাবে?
১। ইনপুট ৪ কল দিয়েছে F(৩) এবং F(২) কেঃ এই ধাপে কল হল ২টা
২। এরপর F(৩) কল দিয়েছে F(২) এবং F(২) কে, আবার F(২) [যেটা ৪ এর কলে পেয়েছি] কল করছে F(১) এবং F(০) কে, এই ধাপে কল হল ৪ টা।
৩। F(২) [যেটা F(৩) এর কলে পেয়েছি] সেটা কল করছে F(১) এবং F(০) কে, এই ধাপে কল হল ২ টা।
সর্বমোট কলঃ ২ + ৪ + ২ = ৮।
উপরের ছবি থেকে আমরা দেখতে পাই একটা নাম্বার সমসময় এর পূর্বের দুইটা নাম্বারকে কল করছে। এই থেকে আমরা বলতে পারি একটা নাম্বারের জন্য একটা ফাংশনকে কল করার সংখ্যা এর পূর্বের দুইটা নাম্বারের কলের সংখ্যা + ২।
উদাহরনঃ
উদাহরনঃ
call(0) = 0
call(1) = 0
call(2) = call(0) + call(1) + 2 = 0 + 0 + 2 = 2
call(3) = call(2) + call(1) + 2 = 0 + 2 + 2 = 4
call(4) = call(3) + call(2) + 2 = 4 + 2 + 2 = 8
call(5) = call(4) + call(3) + 2 = 8 + 4 + 2 = 14
তাহলে আমরা লিখতে পারিঃ
1
| call(n) = call(n-1) + call(n-2) + 2 |
সম্পূর্ন ফাংশনঃ
1
2
3
4
5
6
7
8
9
10
11
| int call(int n){ if(n == 0 || n == 1) { return 0; } else { return call(n-1)+call(n-2)+2; }} |
C/C++:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| #include <bits/stdc++.h>using namespace std;int call(int n){ if(n == 0 || n == 1) { return 0; } else { return call(n-1)+call(n-2)+2; }}int main(){ int n; while(scanf("%d", &n) == 1) { printf("Total calls = %d\n", call(n)); } return 0;} |
Java:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| import java.util.Scanner;public class Main{ static int call(int n) { if(n == 0 || n == 1) { return 0; } else { return call(n-1) + call(n-2) + 2; } } public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n; while(sc.hasNext()) { n = sc.nextInt(); System.out.println("Total calls: " + call(n)); } }} |
আশাকরি আজকের পোষ্টটা বুঝতে আপনাদের কোন সমস্যা হয়নি।






No comments